8 клас - геометрія - урок № 10 ( асинхронно )

Геометрія 8 клас

Тема: Площа трапеції

Мета уроку :

1) Повторити теорему Піфагора

2) Ознайомитися з формулою площі трапеції

3) Оволодіти методикою розв’язування задач на знаходження площі трапеції.

Перед тим, як ми почнемо з вами працювати, я хочу нагадати вам, що мені треба надсилати конспект класної роботи, до якого входять: 

1) конспекти відеоуроків( я оцінюю якість і грамотність їх оформлення);

2) виписані і прописані формули;

3) мої рекомендації.

Потім ви надсилаєте мені свої домашні завдання з рисунками і поясненнями.

Почнемо наш урок, як було зазначено, з повторення теореми Піфагора. Увага: починаємо оформлення класної роботи.

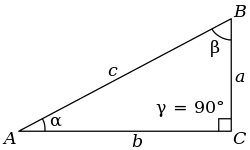
 І так, теорема Піфагора застосовується лише в прямокутному трикутнику. Розглянемо такий приклад. Нехай задано  прямокутний трикутник АСВ.

У цьому трикутнику відомі катети АС = 8, ВС = 4. Треба знайти гіпотенузу АВ.

Розв’язання

Як відомо, квадрат гіпотенузи дорівнює сумі квадратів катетів, тобто, 

Нехай тепер в трикутнику відомі гіпотенуза АВ = 15 і катет ВС = 9. Знайти треба інший катет АС. Застосуємо теорему Піфагора.

Відповідь. 12.

Зараз ви заповните таблицю, в якій треба знайти невідомі сторони прямокутного трикутника АВС. Або перед таблицею, або після ви записуєте розв’язки, аналогічно тому, як це зробила я.

Катет АС	Катет ВС	Гіпотенуза АВ
12	5	?
6	3	?
15	?	20
?	5	14

Учні 1 – 2 груп, крім таблиці, розв’язують такі задачі:

За умовою задачі АF – висота, що проведена до бічної сторони ВС. СF = 12см. Рекомендую двічі застосувати теорему Піфагора: спочатку для трикутника ACF, а потім для трикутника AFB.

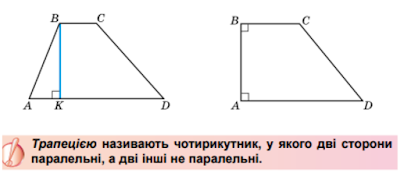
 Переходимо тепер до другої частини нашого уроку. Ми повинні ознайомитися з формулою площі трапеції, але спочатку пригадаємо, що собою являє трапеція.

 На першому рисунку зображено довільну трапецію, на другому – прямокутну. Є ще рівнобічна трапеція.

Ви прослухаєте відеоурок №1 і розглянете декілька способів знаходження площі трапеції.

Ви прослухаєте відеоурок №2,  зробите конспект, але розглядаєте не всі задачі, а по № 960 включно.

А от працювати з матеріалом, який представлено у відеоуроці №3 будуть лише учні 1 – 2 груп

І на завершення уроку ви заповните таблицю, представивши розв’язки або до таблиці, або після.

Зауваження

 Домашнє завдання ви оформлюєте окремо після класної роботи.