8 клас - геометрія - асинхронно
Шановні восьмикласники!
Ми продовжуємо роботу і наступна тема, над якою ми працюємо – це Площа трикутника
Мета: Продовжити знайомство з
формулами для знаходження площі трикутника
План , за яким ви працюєте.
1) Двічі слухаєте вказані відеоуроки:
- відеоурок 1 - натисніть сюди
- відеоурок 2 - натисніть сюди
- відеоурок 3 - натисніть сюди
- відеоурок 4 - натисніть сюди
2) Слухаєте третій раз і робите конспект.
3) Виписуєте усі формули в зошит для правил, і кожну формулу в робочому зошиті прописуєте 5 разів.
5) Надсилаєте заповнені таблиці мені на перевірку до 24.04 включно.
Знаходження площі трикутника за стороною і висотою, що проведена до цієї сторони
Якщо сторона, яку, наприклад, можна позначити через а, дорівнює 14 см, а висота, що проведена саме до цієї сторони h = 9 см, то площа
Знайдіть площу за стороною і висотою
Сторона а
|
Висота h
|
Площа S
|
0,8
|
О,6
| |
10
|
9
| |
1,2
|
0,5
|
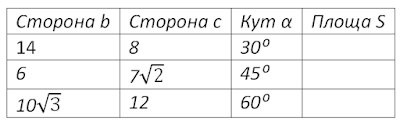
Якщо в трикутнику відомі дві сторони, які можна позначити як а і b, а кут, який утворюють ці сторони позначити як α, то площу цього трикутника можна визначити як половину добутку довжин цих сторін на синус кута між ними, тобто:
Зауваження: довжини сторін можна позначати не тільки як a і b, но і b, c
Взірець.
Заповніть тепер наступну таблицю.
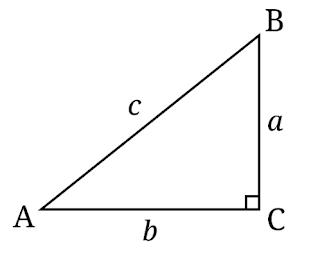
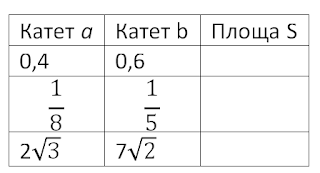
Розглянемо тепер прямокутний трикутник. Ви вже знаєте, що його площа дорівнює половині добутків катетів. Якщо один із катетів позначити як a, а другий - як b, то його площа:
Заповніть наступну таблицю:
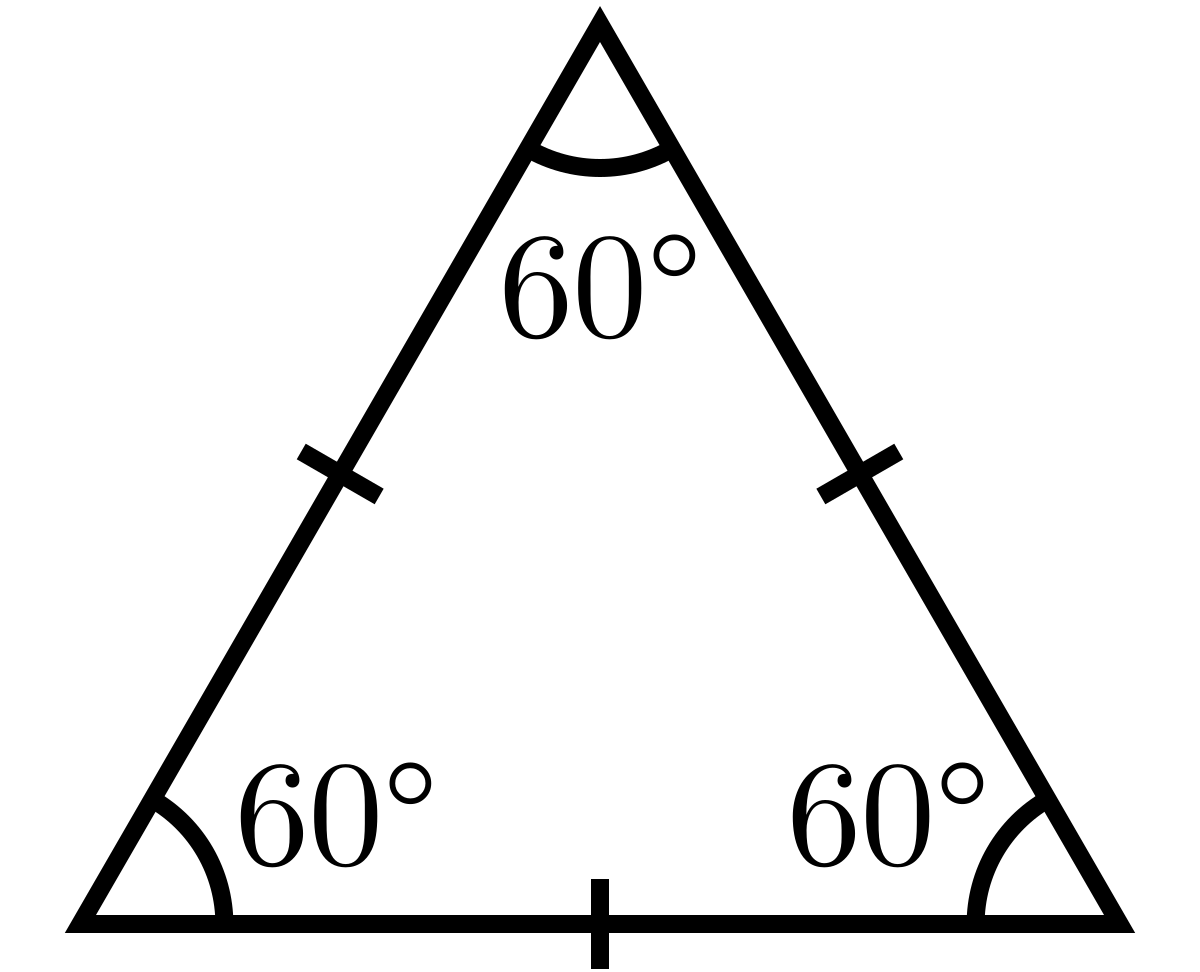
Трикутник, у якого всі сторони і всі кути рівні між собою, називається рівностороннім або правильним.
Позначимо сторону цього трикутника через a. Площу знайдемо як половину добутку двох сторін на синус кута між ними.
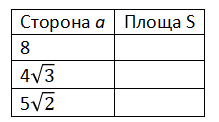
Таким чином, площа правильного трикутника зі стороною а знаходиться за формулою:
Приклад:
Знайдіть площу правильного трикутника зі стороною а заповніть таблицю:
Прослухавши відеоурок, ви дізналися: якщо в трикутнику відомі довжини усіх його сторін, які ми позначаємо а, b, c, то площу такого трикутника краще всього знаходити за формулою Герона.
Розглянемо приклад.
Нехай а = 6, b = 8, c = 10. Знайти площу цього трикутника.
Приклад №2.
Приклад №2.
a =7, b = 6, c = 9. S = ?
Тепер за даними взірцями знайдіть площі заданих трикутників і результат занесіть у таблицю.
Сторона а
|
Сторона b
|
Сторона с
|
Площа S
|
4
|
6
|
8
| |
12
|
5
|
13
| |
15
|
25
|
ВАЖЛИВА ІНФОРМАЦІЯ!
Виконані завдання висилайте на цей адрес:
Виконані завдання висилайте на цей адрес:
kononovaolena@gmail.com
Чекаю на ваші розв'язки.
Комментарии
Отправить комментарий